3.6. Определить момент инерции J тонкого однородного стержня длиной l = 30 см и массой т = 100 г относительно оси, перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоящую от конца стержня на 1/3 его длины.
Дано:
Решение:
l = 0,3 м
т = 0,1 кг
J – ?
Ответ: 3×10-3 кг×м2 ; 0,75×10-3 кг×м2 ; ×10-3 кг×м2
3.7. Определить момент инерции J тонкого однородного стержня длиной l = 60 см и массой т = 100 г относительно оси, перпендикулярной ему и проходящей через точку стержня, удаленную на а = 20 см от одного из его концов.
Дано:
Решение:
l = 0,6 м
т = 0,1 кг
а = 0,2 м
J – ?
Ответ: 4×10-3 кг×м2
3.8. Вычислить момент инерции J проволочного прямоугольника со сторонами а = 12 см и b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью t = 0,1 кг/м.
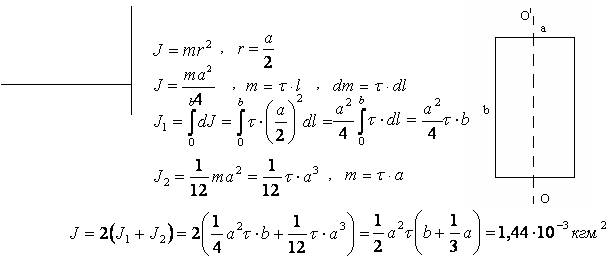Дано:
Решение:
а = 0,12 м
b = 0,16 м
t = 0,1 кг/м
J – ?
Ответ: 1,4×10-3 кг×м2
3.9. Два однородных тонких стержня: АВ длиной l1 = 40 см и массой m1 = 900 г и CD длиной l2 = 40 см и массой т2 = 400 г скреплены под прямым углом (см. рис. ниже). Определить момент инерции J системы стержней относительно оси ОО', проходящей через конец стержня АВ параллельно стержню CD.
Дано:
Решение:
l1 = 0,4 м
m1 = 0,9 кг
l2 = 0,4 м
т2 = 0,4 кг
J – ?
Ответ: 0,048 кг×м2 ; 0,064
кг×м2 ; 0,112 кг×м2
3.10. Решить предыдущую задачу для случая, когда ось ОО¢ проходит через точку А перпендикулярно плоскости чертежа.
Дано: Решение:
l1 = 0,4
м
m1 = 0,9 кг
l2 = 0,4 м
т2 = 0,4 кг
Ответ: 0,114 кг × м2