1.31.
По окружности радиусом R = 5 м равномерно
движется материальная точка со скоростью v = 5
м/с. Построить графики зависимости длины пути s и
модуля перемещения 
от времени t. В момент
времени, принятый за начальный (t = 0), s(0) и 
считать равными нулю.
Дано:
Решение:
R = 5 м
v = 5 м/с
t = 0
s(0) = 0
= 0
s()– ?
s(t) – ?
Ответ:
1.32.
За время t = 6 с точка прошла путь, равный
половине длины окружности радиусом R = 0,8 м.
Определить среднюю путевую скорость 
за это время и модуль
вектора средней скорости 
.
Дано:
Решение:
t = 6 с
R = 0,8 м
– ?
– ?
Ответ:
1.33.
Движение точки по окружности радиусом R = 4 м
задано уравнением[1]
, где
А = 10 м, В = –2 м/с, С = 1 м/с2. Найти
тангенциальное 
, нормальное 
и полное а ускорения точки в момент времени t = 2 с.
Дано:
Решение:
R = 4 м
А = 10 м
В = –2 м/с
С = 1 м/с2
– ?
– ?
а – ?
Ответ: 2 м/с2, 1 м/с2 , 2,24 м/с2.
1.34.
По дуге окружности радиусом R = 10 м движется
точка. В некоторый момент времени нормальное ускорение точки 
= 4,9 м/с2; в этот
момент векторы полного и нормального ускорений образуют угол 
60°. Найти скорость v и тангенциальное ускорение 
точки.
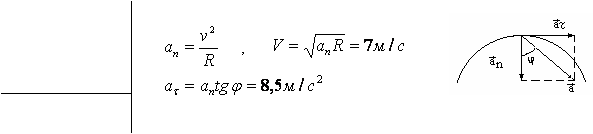Дано:
Решение:
R = 10 м
= 4,9
м/с2
60°
v - ?
- ?
Ответ: 7 м/с , 8,5 м/с2.
1.35.
Точка движется по окружности радиусом R = 2 м
согласно уравнению1 
, где A = 2 м/с3. В какой момент времени t нормальное ускорение точки будет равно
тангенциальному 
? Определить полное ускорение а в этот момент.
Дано:
Решение:
R = 2 м
A = 2 м/с3
=
t – ?
а – ?
Ответ: t = 0,872 с , a = 14,8 м/с2